
Keby sa vás niekto spýtal, čo je to vlastne čiara, čo by ste mu povedali? Úsečka? Priamka? Kružnica? Raz je to úsečka, inokedy kus priamky či kružnice… No väčšinou niečo úplne iné.
Mladí študenti sa v rámci prednášky O krivkách, ktorá sa odohrala počas podujatia Žilinská detská univerzita, dozvedeli aj tieto zaujímavé fakty. Organizovala ho Žilinská univerzita v Žiline (UNIZA) vo svojich priestoroch v termíne 9. – 13. júla 2018. Jej cieľom bolo vzbudiť zvedavosť a záujem detí o objavovanie sveta okolo nich. Štrnásty ročník populárnej Žilinskej detskej univerzity navštívilo 138 detí (77 detí v kurze bakalárik a 61 v kurze inžinierik).
„V matematike, ale najmä v geometrii a vo všetkých vedách s ňou súvisiacich, sú čiary veľmi dôležité. Teda aspoň niektoré. Nemám teraz na mysli úsečky a priamky, ale skôr také tie všelijako pokrivené čiary. Budeme ich nazývať krivky. Keby sme chceli v tejto chvíli napísať, čo to vlastne krivka je, asi by to nebol dobrý nápad. Presná definícia krivky by si vyžadovala veľmi hlboké a podrobné poznatky z mnohých častí geometrie, matematiky či fyziky,“ odznelo počas prednášky Mgr. Miroslavy Konrádovej O krivkách.
Za krivku považovali trajektóriu – dráhu pohybujúceho sa bodu. „Aby sme si mohli niektoré krivky nielen nakresliť, teda zostrojiť, ale aj matematicky popísať, dohodneme sa, že bod, o ktorom hovoríme, sa pohybuje v nejakom čase t. Keďže dráha nášho bodu sa mení spolu s pribúdajúcim časom, nazveme hodnotu t parametrom. Krivku potom môžeme považovať za nekonečnú množinu bodov, ktorých poloha závisí od jediného parametra t. Hovoríme, že krivka je jednoparametrická sústava bodov a matematicky by sme túto skutočnosť vyjadrili rovnicami pre jednotlivé súradnice (x = f(t), y = g(t)).“
Ako uviedla prednášajúca, krivky delíme z rôznych pohľadov, napríklad na rovinné a priestorové. Rovinnou krivkou je taká krivka, ktorej všetky body ležia v jednej rovine. Ňou je napríklad už spomínaná kružnica. V opačnom prípade hovoríme, že krivka je priestorová. Takou je napríklad strunka v „prepisovačke“. Ďalšie rozdelenia kriviek vychádzajú z iných kritérií. Poznáme napríklad krivky empirické, teda tie, pre ktoré poznáme graf, ale nevieme ich matematicky vyjadriť a potom krivky matematické, teda tie, ktoré sú vyjadrené matematickými rovnicami a podobne.
Mladí účastníci sa na začiatok dozvedeli, že postačí, ak sa zoznámia s niektorými najznámejšími rovinnými krivkami. „Aby sme sa s krivkami a ich vlastnosťami oboznámili bližšie, budeme si ich modelovať. Potrebujeme ceruzku, papier, mäkkú podložku pod papier, špendlíky, pevnejší drôtik, pevnú niť alebo špagátik, vrchnáky zo zaváracej fľaše, CD-čka… alebo veľmi dobrú predstavivosť. Začneme tým, že si zadefinujeme niektoré základné pojmy, ktoré budeme neskôr používať.“
Mladí poslucháči si následne mali predstaviť ľubovoľnú jednoduchú krivku k v rovine (mohli si ju nakresliť alebo vymodelovať z drôtika). Každú priamku s, ktorá pretína túto krivku, budeme nazývať sečnicou krivky a body, v ktorých priamka s krivku k pretne, nazveme priesečníky priamky s krivkou. Vyberme si z krivky len úsek, na ktorom má s priamkou práve dva spoločné body A, B. Ak si túto situáciu vymodelujete z drôtikov, priviažte si jemne „priamku“ o „krivku“ v ich priesečníkoch. Pozrime sa, čo sa stane s priamkou s, keď začneme bod A po krivke približovať k bodu B až do chvíle keď splynú. V takomto prípade má krivka s priamkou jediný spoločný bod, mení sa zo sečnice s na dotyčnicu t a priesečníky splynú do bodu, ktorý nazveme dotykový bod a označíme ho T. V odborných knihách sa o priamke t (dotyčnici) dočítate ako o limitnej polohe priamky s (sečnice). Úsečku AB nazývame tetiva krivky k. Kolmicu n, zostrojená na dotyčnicu t v dotykovom bode T krivky a ležiaca v rovine krivky k nazývame normálou krivky k v bode T.
Prednáška pokračovala, že kužeľosečky sú jedny z najznámejších rovinných kriviek. Ako už ich názov napovedá, vznikajú „preseknutím“, teda rezom kužeľa. Pod kužeľom nie je podľa prednášajúcej vhodné predstavovať si taký ten „cestársky“ kužeľ, ktorý sa na zemi začína a vrcholom končí. „My si kužeľom pomenujeme útvar, ktorý vznikne, keď dva takéto kužele vo vrchole zlepíme. Presnejší názov pre takýto útvar je dvojkužeľ. Modelovanie takého útvaru je veľmi jednoduché: vezmite si vrchnák v tvare kruhu na zaváraciu fľašu ľubovoľnej veľkosti, zviažte asi 20 špajdlí v strede niťou a postavte ich na stôl do vrchnáka tak, aby sa dotýkali jeho stien. Na obrázku vidíme, ako by sme potom rozrezali kužeľ tak, aby vznikli jednotlivé kužeľosečky.“
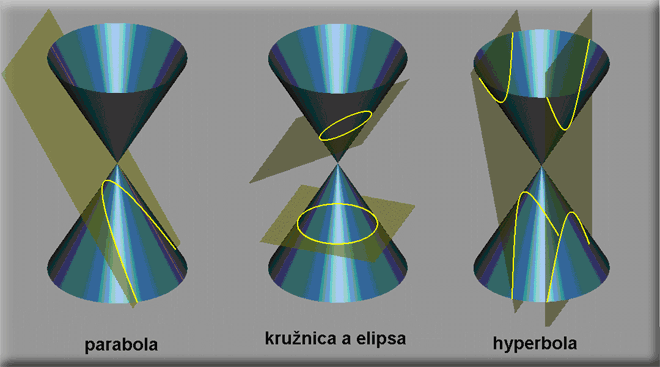
Pomenovanie kužeľosečiek – parabola, hyperbola a elipsa zaviedol vo svojich ôsmych knihách o kužeľosečkách okolo roku 200 p. n. l Apollónius z Pergy. Analytickú geometriu kužeľosečiek rozpracoval R. Descartes vo svojej knihe La Geometrie a zaujímavú prácu o bodových konštrukciách kužeľosečiek napísal už Ibrahím Ibn Sinán.
Ešte mnoho iného zaujímavého sa na tému kriviek dozvedeli mladí účastníci Žilinskej detskej univerzity.
*********************************************
Podujatie Žilinská detská univerzita (ŽDU) organizuje Elektrotechnická fakulta Žilinskej univerzity v Žiline (UNIZA) už od roku 2005, pričom každoročne nadväzuje na výnimočnú aktivitu v oblasti propagácie vedy a techniky v spoločnosti medzi najmladšími žiakmi základných škôl. ŽDU je založená na popularizácii prírodovedných a technických predmetov, hre, interaktivite a tvorivosti, takže základ ostáva rovnaký – pre kurz bakalárik vysvetľovanie prírodných zákonov, jednoduchých princípov a pre kurz inžinierik – aplikácia zákonov do praxe. „UNIZA sa rada aj týmto spôsobom otvára verejnosti. Snažíme sa pritiahnuť deti už od ranného veku k vede a technike, aby v nej objavili krásu a zmysel a mohli ju raz študovať,“ vyjadril sa prof. Ing. Jozef Jandačka, PhD., rektor UNIZA.
Zdroj informácií a fotografií:
https://zdu.uniza.sk/prednasky
Spracovala: Slávka Cigáňová (Habrmanová), NCP VaT pri CVTI SR
Uverejnila: VČ


